我們介紹完了 priority Queue，接著要介紹的是 "double-ended" priority Queue

除了有新增元素之外，提供「提出最低優先權元素」及「提出最高優先權元素」2種操作。
而今天要來介紹的就是最適合用來實作他的資料結構。

1. Min-Max Heap

是一棵 complete binary tree，使用 Array 儲存。可為空，若非空則：

1. min-level 及 max-level 交替出現
2. 若節點 x 位於 min-level，則以 x 為 root 之 tree，皆大於 x。
3. 若節點 x 位於 max-level，則以 x 為 root 之 tree，皆小於 x。
4. 整個 heap 的 root 必位於 min-level

圖例：wiki

為何適合用來實作 double-ended priority queue?

因為當這樣設計後：min-value 在 root，max-value 在 level-2 節點的最大值。全都是 O(1) 時間

insert X into min-max heap

1. 一樣將新節點加入最後的位置，維持 complete binary tree
2. 將 x 的 parent 設為 p
3. 若 p 位於 min-level，檢查 x 是否大於 p，若無則交換 x & p。若 x > p 則不須交換。
4. 重複檢查 x 的祖父節點是否滿足 level 定義。也就是說，x 目前位於哪個 level，就調整該 level 即可。
5. 若 p 位於 max-level，則全反過來操作

用個例子來說明：

delete min-value

1. 取出 root 值，並將最後一顆節點補上，維持 complete binary tree
2. 接著判斷三種情況。若 root 無子點，則直接完成；若 root 有子點，但沒有孫節點，則將最小值置於 root，即完成。
   第三種情形：如果 root 有孫節點，則令 k 為孫節點最小值，再令 k 的 父親為 p，接著若 x > k 則兩者位置及值互換，互換後，若 p < x 則進行 p 跟 x 的「值」互換，此時 x 必位於 min-level，重複上述動作判斷，直到 heap 滿足定義。

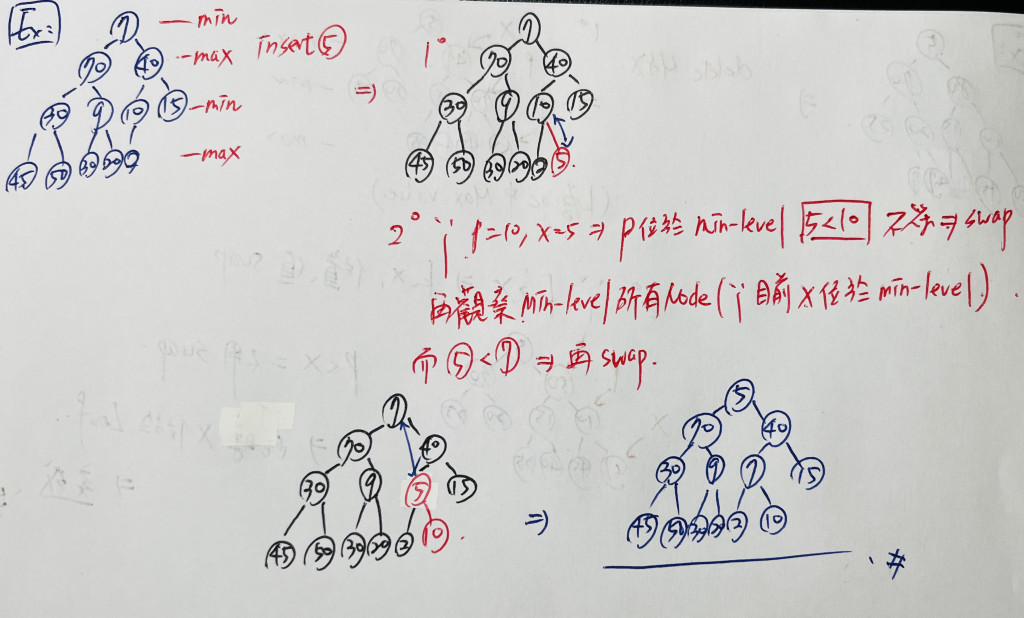
一樣來說明：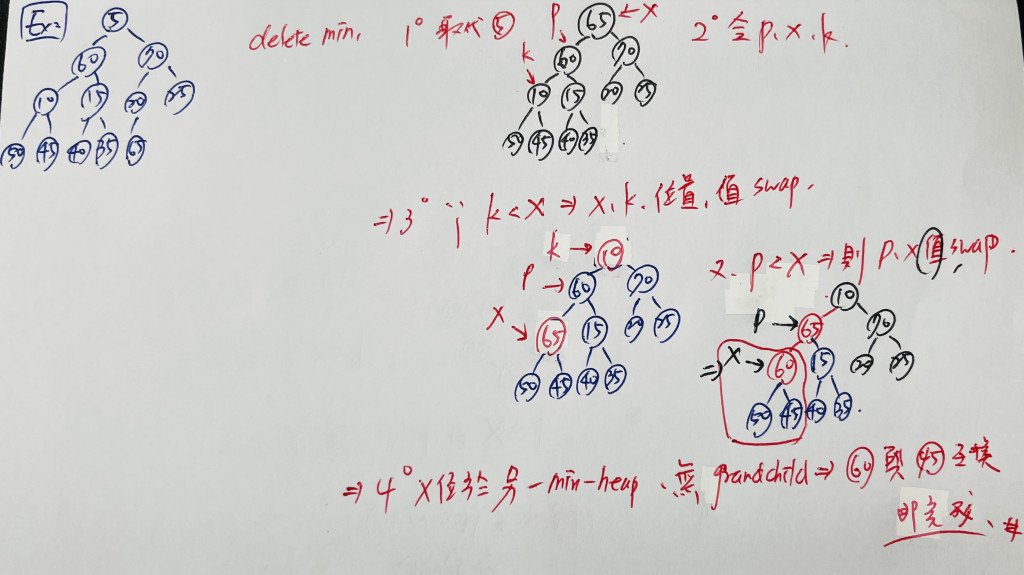

delete max-value

delete max-value 就是 delete min 的完全反向操作，在一個 MAX-MIN Heap 進行調整。當然，並沒有這個名詞，不過方便說明則這樣稱呼。

我們直接來看範例：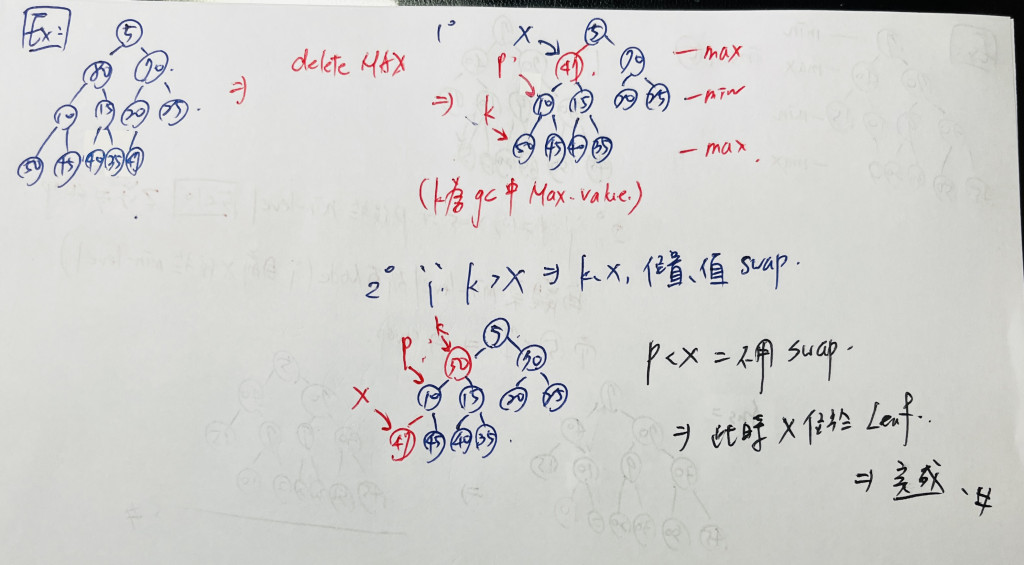

2. Deap 雙邊堆積

接下來兩個比較少見的資料結構，都介紹定義而已，並附上操作的資料來源。

資料來源：https://www.tutorialspoint.com/deaps-in-data-structure

是一棵 complete binary tree，使用 Array 儲存。可為空，若非空則：

1. root 不放資料
2. root 左子樹是min-heap，右子樹是max-heap
3. 若 i 在 min-heap 中，則其必小於等於其在 max-heap 對應點 j (i <= j)
4. 何謂對應點？將 min-heap 及 max-heap 視為相同結構，位於相同位置的點，則為對應點，若 i 之對應點 j 不存在，則令該位置之 parent 為 對應點 j。

圖中 A 和 B 為對應位置。

Symmetric min-MAX heap (SMMH)

資料來源：https://www.tutorialspoint.com/symmetric-min-max-heaps

是一棵 complete binary tree，使用 Array 儲存。可為空，若非空則：

1. root 不放資料
2. 遵守三個規則：
   p1: 左兄弟必小於等於右兄弟
   p2: 若某點 i 有 grandparent，則grandparent 的 Left child 必小於等於 i
   p3: 若某點 i 有 grandparent，則grandparent 的 Right child 必大於等於 i

總結

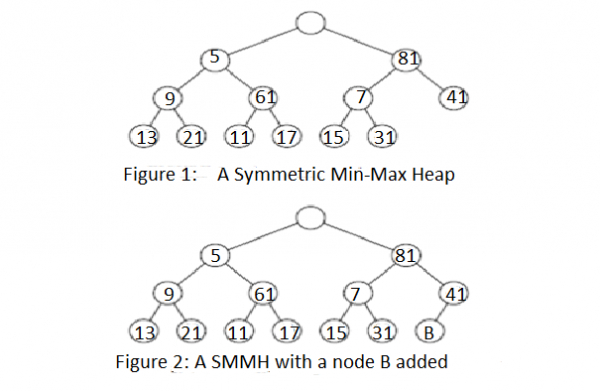
我們介紹完了所有的 Binary tree 結構，也介紹完了 priority queue 的實作。
接著要來進入 external search 的章節。明天來介紹 m-way search tree